来源

https://blog.csdn.net/g0ose/article/details/54933038

奇偶规则和非零缠绕规则

多边形的内外

这个判断与多边形是否是自相交有关

在图形学中判断一个点是否在多边形内，若多边形不是自相交的，那么可以简单的判断这个点在多边形内部还是外部；

若多边形是自相交的，那么就需要根据非零缠绕规则和奇-偶规则判断多边形的外部和内部。

判断依据

判断多边形是否是自相交的：多边形在平面内除顶点外还有其他公共点

实现方法

内-外测试

不自交的多边形：多边形仅在顶点处连接，而在平面内没有其他公共点，此时可以直接划分内-外部分。

自相交的多边形：多边形在平面内除顶点外还有其他公共点，此时划分内-外部分需要采用以下的方法。

奇-偶规则

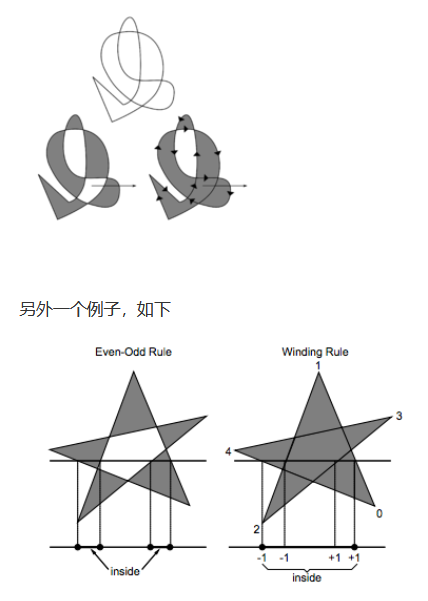
(1)奇-偶规则（Odd-even Rule）：奇数表示在多边形内，偶数表示在多边形外

从任意位置p作一条射线，若与该射线相交的多边形边的数目为奇数，则p是多边形内部点，否则是外部点。

非零缠绕规则

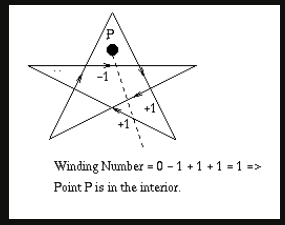
(2)非零缠绕规则（Nonzero Winding Number Rule）：若环绕数为0表示在多边形内，非零表示在多边形外
首先使多边形的边变为矢量。将环绕数初始化为零。再从任意位置p作一条射线。当从p点沿射线方向移动时，对在每个方向上穿过射线的边计数，每当多边形的边从右到左穿过射线时，环绕数加1，从左到右时，环绕数减1。处理完多边形的所有相关边之后，若环绕数为非零，则p为内部点，否则，p是外部点。

参考[1]中例子如下，判断点p是否在多边形内，从点p向外做一条射线（可以任意方向），多边形的边从左到右经过射线时环数减1，多边形的边从右往左经过射线时环数加1，最后环数不为0，即表示在多边形内部。

补充：自相交的判断

https://blog.csdn.net/qq_34719188/article/details/108545342

补充2

https://juejin.cn/post/7117039936619937805