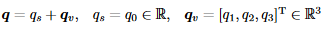参考资料
基本介绍
惯性导航系统是一个自主的、完备的三维航位推算系统。
对于平台式惯导,陀螺稳定平台这一机电结构的存在使得加速度计的物理安装轴线始终跟踪并对齐当地地理坐标系的东向、北向和垂向,这样只需对三个加速度计的测量值按时间做一次和两次积分即可得到载体的速度和位置。
我们课程关心捷联惯性导航系统,即惯性传感器(陀螺和加速度计)直接与载体绑定固联,加速度计的安装轴线不再时刻跟踪当地地理坐标系了。
因此,在做捷联惯性导航计算时要时刻计算出载体相对于参考坐标系(如当地水平坐标系)坐标轴的相对空间朝向关系,即载体的姿态;
从而将加速度计的比力测量值投影变换到参考坐标下,然后,再对其参考系下的比力投影分量进行积分运算解得载体的速度和位置。
这就是完整的捷联惯性导航解算过程,其中载体姿态、速度和位置三组参数的解算过程分别称之为捷联惯性导航的姿态更新、速度更新和位置更新。
由此可见,在捷联惯性导航解算中,求解载体的姿态有两个重要的作用,一是输出载体的姿态这一重要导航参数,二是用于实现加速度计比力测量值的坐标变换。
姿态更新算法是捷联惯性导航算法的核心,对整个系统的解算精度影响最为突出,其作用至关重要。
总结
1.所获取的数据:载体的速度和位置
2.数据处理:
计算出载体的姿态
利用计算出的载体姿态实现相关导航功能
计算出载体的位置和速度
利用计算出的位置和速度姿态实现相关导航功能
载体姿态描述
我们使用向量可以很方便地描述三维空间中载体的速度和位置,但是要描述载体的姿态则没有那么容易。
例如,我们可以说“飞机机头北偏东 30◦,机头相对当地水平面抬升 5◦”这样的话来描述飞机的姿态。
描述姿态的数学语言我们称之为姿态表达式。
四种常用的姿态表达式:包括欧拉角、方向余弦矩阵、四元数和等效旋转矢量。
为什么要介绍多种姿态表达式呢,能只学一种吗?
当然可以,但是后续我们会发现,这四种姿态表达式各有优缺点,综合使用更加方便。
例如,用欧拉角描述载体的空间轴向非常直观,但它却无法用于全姿态导航解算,并且要实现比力测量值的坐标变换,须转换成对应的方向余弦矩阵或四元数;
方向余弦矩阵用于实现向量的投影变换非常方便,但是通过求解方向余弦矩阵或四元数的微分方程来实现姿态解算时都会不可避免地遇到“不可交换性误差”,而这个问题却可以通过使用等效旋转矢量从理论上得到完美的解决。
因此,在实际惯性导航应用中,我们往往会灵活选用多种不同的姿态表达式,取长补短。
当载体运动时,其姿态也随时间变化,那么我们如何描述姿态的变化规律呢?
在实际工程应用中,我们又怎样实现载体姿态的递推计算?
我们常用姿态表达式的时间导数或叫微分方程来描述载体姿态随时间的变化规律,然后通过求解这个微分方程得到载体姿态的递推计算式,从而可编程实现载体姿态的更新计算。
四种姿态表达式
首先给出姿态表达式的定义,然后推导其微分方程,最后求解微分方程得到姿态更新表达式。
在本讲义末尾,我们给出了一个综合使用了多种姿态表达式的惯性导航姿态更新算法示例,以帮助大家从前面繁重的公式推导中抽身出来,避免“只见树木不见森林”
欧拉角法
-
分为静态欧拉角和动态欧拉角两种定义方式
万象死锁问题通常出现在动态定义中
https://www.youtube.com/watch?v=vLDn-ZITDgA
-
所有的轴都跟物体的移动而移动

https://www.youtube.com/watch?v=jRJYtK8BT6U
https://www.youtube.com/watch?v=qqlLshaHqeE
直观理解什么是欧拉角
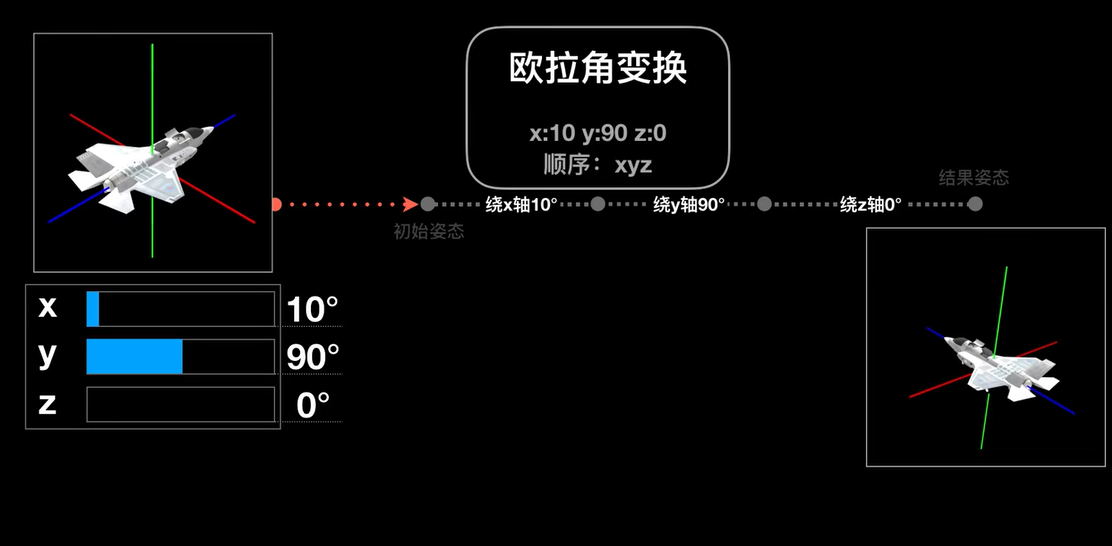
这里描述的是变动一整个过程
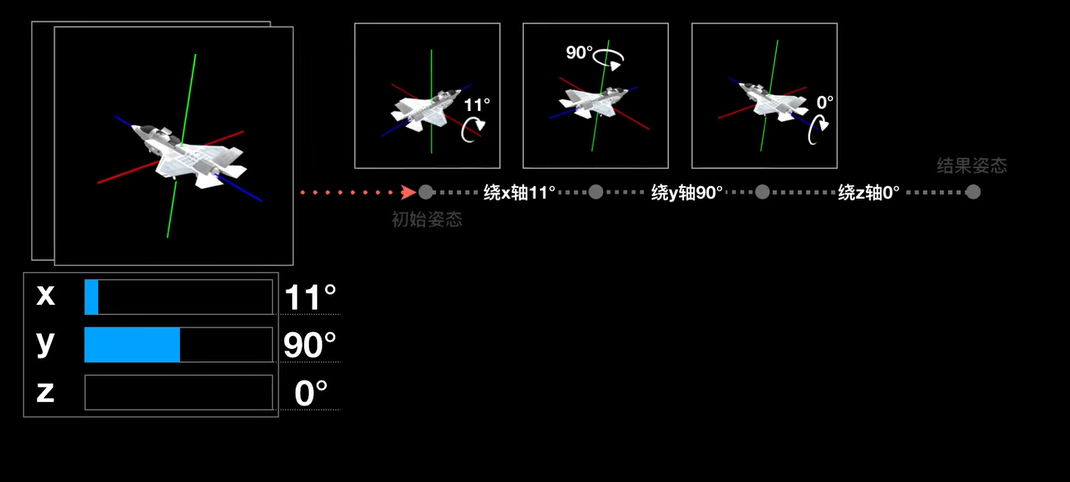
每一个蓝色的xyz条都是飞机从000状态到xyz这三个状态的变换过程
意味着每次数据的调整都是从xyz的顺序从000状态开始调整的,在大多数程序的视线中
描述方式的缺点
-
万向死锁问题
-
旋转顺序不可以交换,这回导致结果的不一致
-
一般解决方案:调整xyz顺序,让x在中间或者 采用另一种描述方案
旋转矩阵/方向余弦矩阵

https://www.youtube.com/watch?v=IOl6GTHhi0A
基本概念介绍与性质
https://www.youtube.com/watch?v=QSdJz4pVDzE
图形化理解基本旋转和基本(后面看不懂)
https://www.youtube.com/watch?v=xY6qOHBf1as
二维旋转矩阵的描述
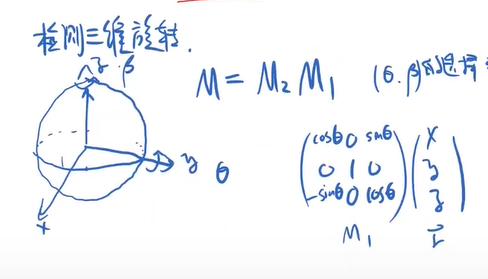
一个经典的几何式子
四元数
四元数基本概念了解
- 用一个向量来表示坐标轴
https://www.youtube.com/watch?v=zjMuIxRvygQ
31的式子实时显示与交互式的模型
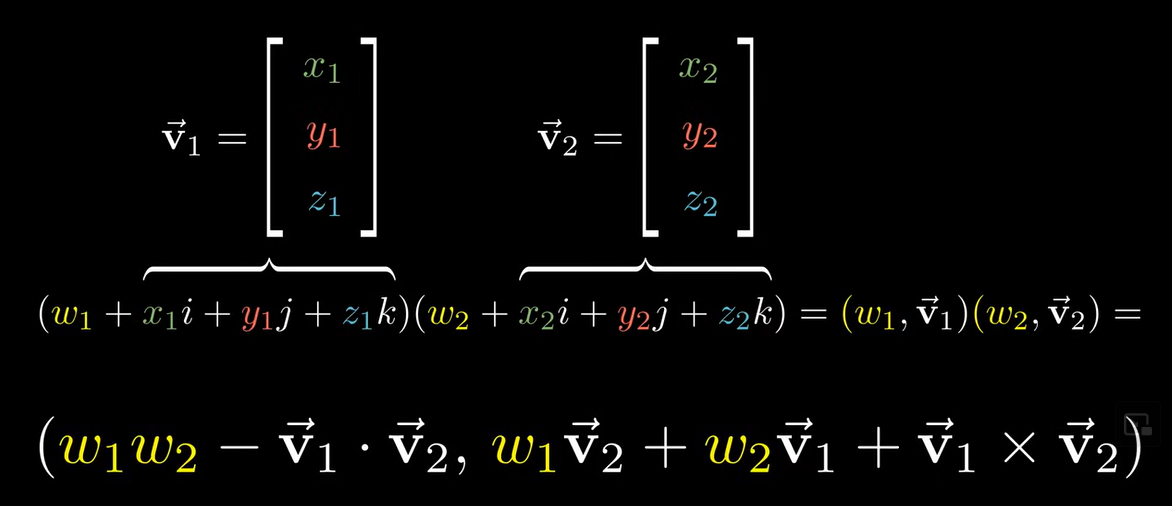
计算和理解的关键式子
https://www.youtube.com/watch?v=d4EgbgTm0Bg
利用立体投影可视化数值
纯数学部分
基本定义形式
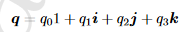
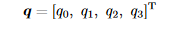
第一个式子中第一个数据是标量,后面都是带方向的矢量
i, j, k 为四元数的三个虚部
1, i, j, k 可以看做四维空间(用符号 H 表示)中的一组单位矢量
第二个式子是四元数的向量形式
等价拆分
数也可以写成标量部分 qs 和矢量部分 qv 之和。
除了基本定义之外的表达形式(三角表示法)


乘法运算
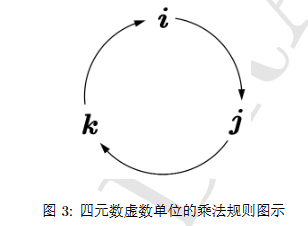
四元数虚数单位之间的乘法有如下特点:单位与单位自己相乘时,表现与复数一样,而两两之间的乘法则与三维向量的外积(叉乘)一样。
利用图 3的图示法容易记住这一乘法规则:按箭头排列的两个单位相乘时,便得到带正号的第三个单位;当反着移动时,便得到带负号的第三个单位。在这样的乘法规则下,两个四元数之积仍为四元数。
基本运算
相等 乘法(不满足交换律 满足乘法结合律) 加法(符合加法分配律)
模
逆
归一
- 乘法

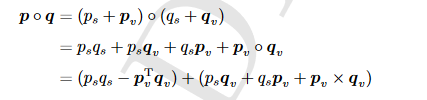

- 几何理解
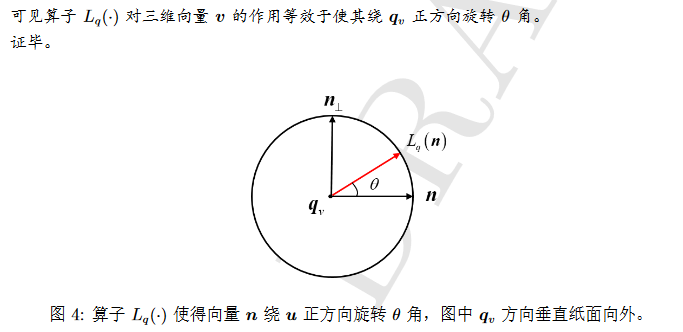
- 相关定理和相关几何理解
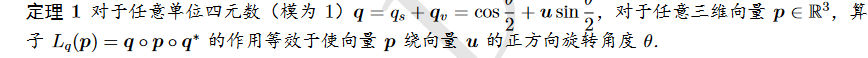
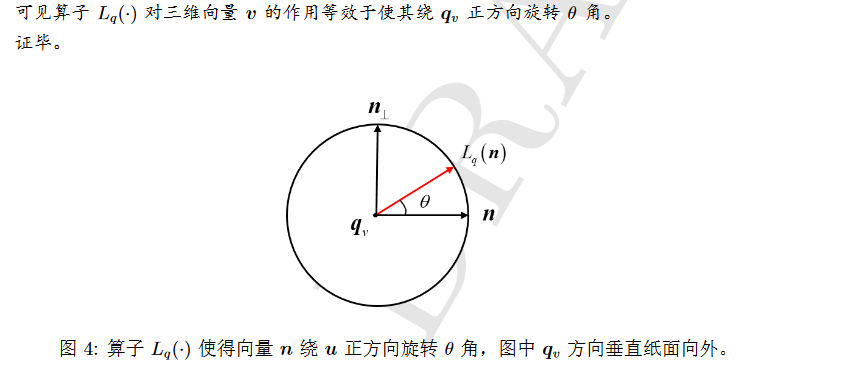
利用四元数+三维向量 进行计算描述一个旋转过程
姿态四元数



等效旋转矢量
欧拉旋转定理(Euler’s rotation theorem)表明,
刚体(可视为直角坐标系)
从一个角位置到另一个角位置的任意转动(这个动作的表示好抽象)总能够
等效于绕一固定轴的一次转动
https://blog.csdn.net/m0_38095099/article/details/105603523#21__8
都是定义和推导
没有图片
也太抽象了