前言

第一遍看到啥写啥

迭代递归

递
归
分治

栈、递归转迭代

/* 使用迭代模拟递归 */
int forLoopRecur(int n) {
    // 使用一个显式的栈来模拟系统调用栈
    stack<int> stack;
    int res = 0;
    // 递：递归调用
    for (int i = n; i > 0; i--) {
        // 通过“入栈操作”模拟“递”
        stack.push(i);
    }
    // 归：返回结果
    while (!stack.empty()) {
        // 通过“出栈操作”模拟“归”
        res += stack.top();
        stack.pop();
    }
    // res = 1+2+3+...+n
    return res;
}

选择方法的考虑

观察以上代码，当递归转化为迭代后，代码变得更加复杂了。尽管迭代和递归在很多情况下可以互相转化，但不一定值得这样做，有以下两点原因。

转化后的代码可能更加难以理解，可读性更差。

对于某些复杂问题，模拟系统调用栈的行为可能非常困难。

总之，选择迭代还是递归取决于特定问题的性质。在编程实践中，权衡两者的优劣并根据情境选择合适的方法至关重要。

时间复杂度

记忆一般的比较

时间复杂度分析要点

输入数据的规模（一般来说是看个数n）
输入数据本身的排序状态

一般分析方法

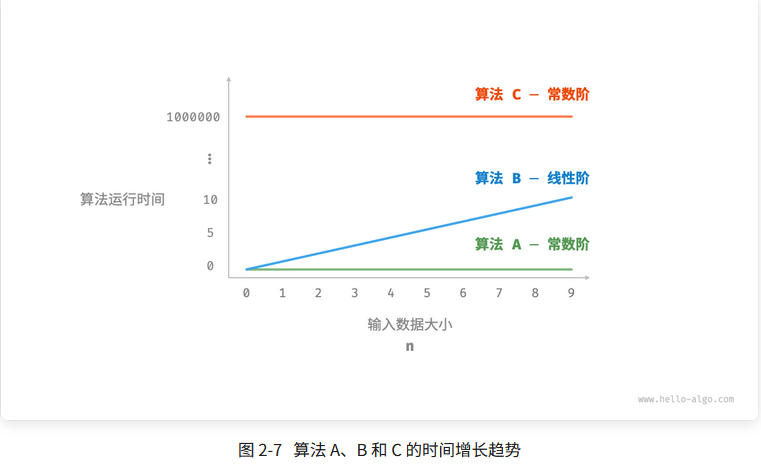
判断该评估方法的优势以及合理性

1.泛而不具体

2.更多的是在评估一种时间增长的趋势，而非实际体量的运行时间（实际中，实际体量非常重要）

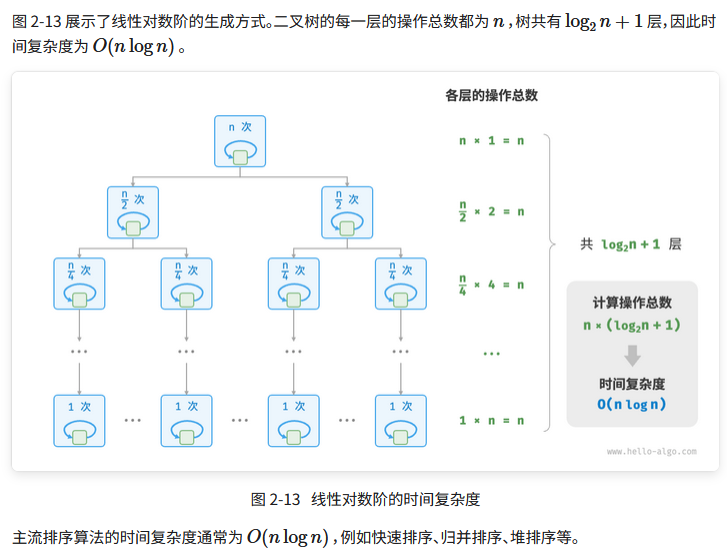
不同类型时间复杂度分析实例

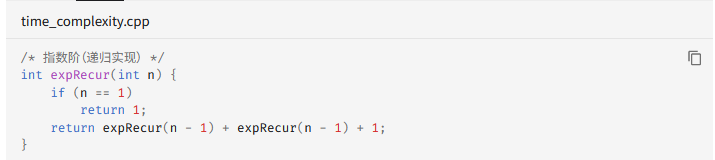
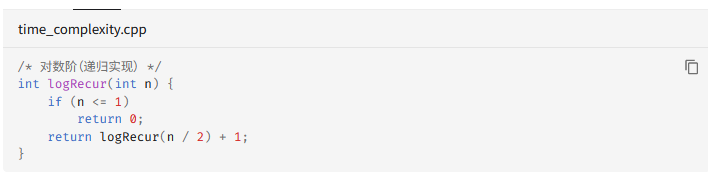
对于递归例子的分析

1.函数内部是否又调用函数本身

2.递归到底最后return 在递什么，又在归什么！

发现一个问题

我将并列出现特征与 *本身结合起来了，这个可不是一个很好的关联关系

递归存在的时候，外塔延申和向内存在是必然的

在递归内部相关n的调用和递归本身指数阶关系也是值得讨论的

看看这个分析路径

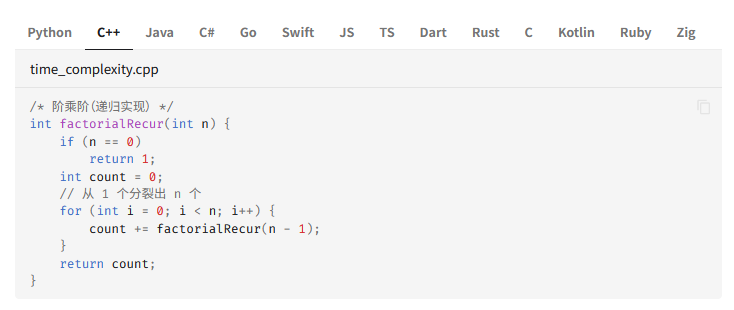
这个例子的话

递归相关的分析变量

第一层的n形态

第二层的形态的数量与n是什么关系是* 2的关系吗？还是 *（n-1）的关系

然后看看层数和n的联系在哪

对数阶/一分为多

平均时间复杂度

特殊数据出现概率导致最好最坏情况出现
平均时间复杂度

空间复杂度

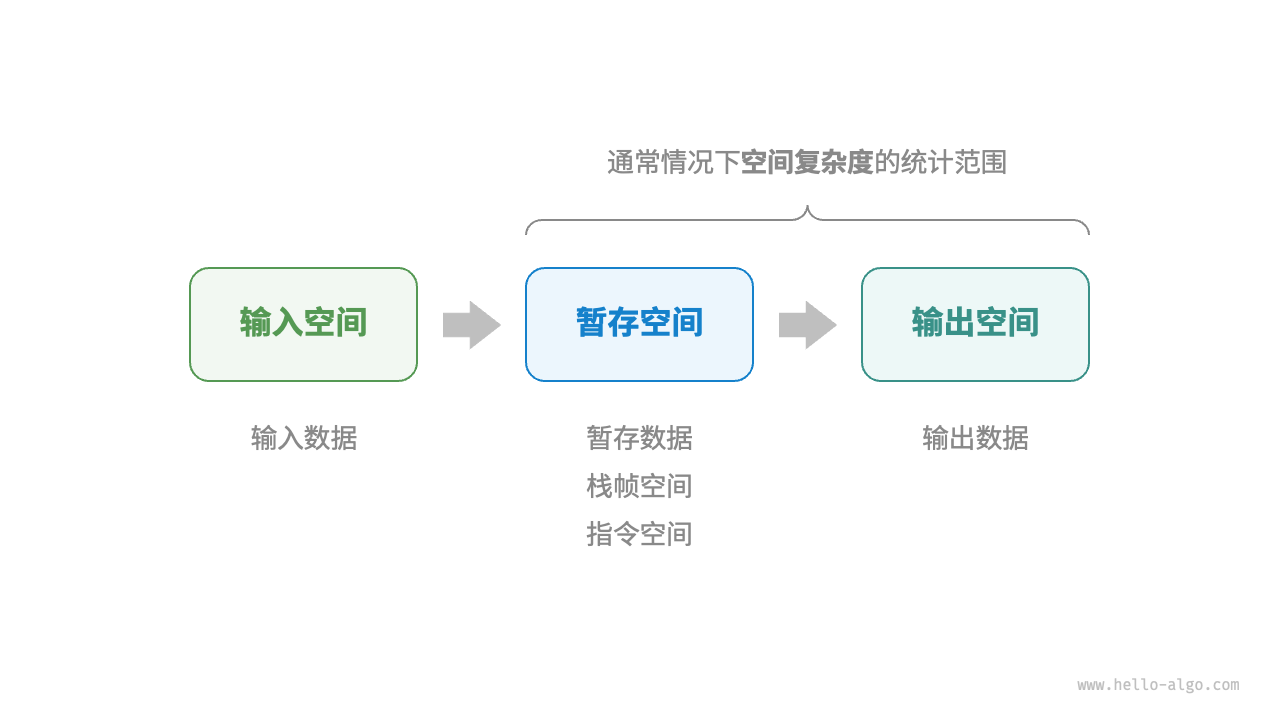
过程中几个涉及空间的概念

算法在运行过程中使用的内存空间主要包括以下几种。

输入空间：用于存储算法的输入数据。
暂存空间：用于存储算法在运行过程中的变量、对象、函数上下文等数据。
输出空间：用于存储算法的输出数据。

一般情况下，空间复杂度的统计范围是==“暂存空间”加上“输出空间”。(不算输入)==

暂存空间可以进一步划分为三个部分。

暂存数据：用于保存算法运行过程中的各种常量、变量、对象等。
栈帧空间：用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧，函数返回后，栈帧空间会被释放。
指令空间：用于保存编译后的程序指令，在实际统计中通常忽略不计。

在分析一段程序的空间复杂度时，我们通常统计暂存数据、栈帧空间和输出数据三部分，如图 2-15 所示。

[ 算法使用的相关空间

/* 结构体 */
struct Node {
    int val;
    Node *next;
    Node(int x) : val(x), next(nullptr) {}
};

/* 函数 */
int func() {
    // 执行某些操作...
    return 0;
}

int algorithm(int n) {        // 输入数据
    const int a = 0;          // 暂存数据（常量）
    int b = 0;                // 暂存数据（变量）
    Node* node = new Node(0); // 暂存数据（对象）
    int c = func();           // 栈帧空间（调用函数）
    return a + b + c;         // 输出数据
}

一般分析角度

空间复杂度的推算方法与时间复杂度大致相同，只需将统计对象从“操作数量”转为“使用空间大小”。
只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。
在递归函数中，需要注意统计栈帧空间。

int func() {
    // 执行某些操作
    return 0;
}
/* 循环的空间复杂度为 O(1) */
void loop(int n) {
    for (int i = 0; i < n; i++) {
        func();
    }
}
/* 递归的空间复杂度为 O(n) */
void recur(int n) {
    if (n == 1) return;
    return recur(n - 1);
}

分析实例

分析空间不是说看 n不在哪里就可以了，要看哪些东西的执行次数和 n 有关

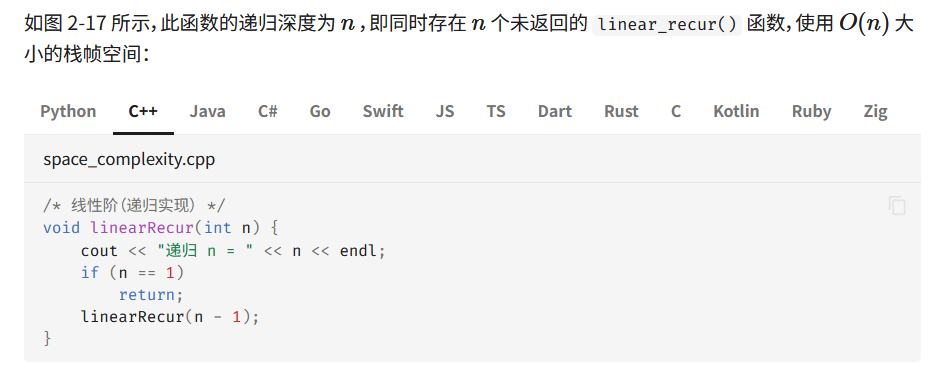
递归实例的分析，深度和空间的关系

二叉树

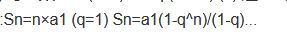
对数阶

分治

递归层面调用多少层递归层也是一个很重要衡量空间复杂度的情况

权衡时间与空间

理想情况下，我们希望算法的时间复杂度和空间复杂度都能达到最优。然而在实际情况中，同时优化时间复杂度和空间复杂度通常非常困难。

降低时间复杂度通常需要以提升空间复杂度为代价，反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”；反之，则称为“以时间换空间”。

选择哪种思路取决于我们更看重哪个方面。在大多数情况下，时间比空间更宝贵，因此“以空间换时间”通常是更常用的策略。当然，在数据量很大的情况下，控制空间复杂度也非常重要。

基本数据类型

基本数据类型提供了数据的“内容类型”，而数据结构提供了数据的“组织方式。
基本数据类型:int、float、double、char、bool…
基本数据类型的取值范围取决于其占用的空间大小。

byte占用的空间是1字节=8bit，可以表示2^8个数字

int占用的空间是4字节=4*8bit，可以表示…

数据结构分类

逻辑

线性
非线性
- 树形结构
- 网状结构

空间

基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度

的数组）等。

基于链表可实现：栈、队列、哈希表、树、堆、图等。

静动

链表在初始化后，仍可以在程序运行过程中对其长度进行调整，因此也称“动态数据结构”。数组在初始化后长度不可变，因此也称“静态数据结构”。值得注意的是，数组可通过重新分配内存实现长度变化，从而具备一定的“动态性”。

数组

理解

一般操作

适合解决问题的特点

1.随机访问

2.排序与搜索

3.查找表/映射关系

4.线性代数相关运算

~~5.其他数据结构基础~~

优点：随机访问、缓存局部、空间效率高
局限性：插入、删除不行，长度变化是个问题，空间容易造成浪费

插入、删除、查找、遍历、扩容
插入即移动之后的数据+插入
删除即移动之后的数据+删除

时间复杂度：

链表

行为：初始化、插入、删除、访问、查找
基本类型

单向链表：

环形链表：

双向链表：
链表典型应用

单向链表

单向链表是一种常见的链表结构，每个节点包含一个指向下一个节点的指针。

资源管理：单向链表可以用来管理资源，例如内存分配中的空闲块链表，通过将空闲的内存块连接成一个链表，可以方便地进行分配和释放。
队列实现：单向链表可以用于实现队列（FIFO）的数据结构，通过在链表的尾部添加元素，并在链表的头部移除元素，可以实现高效的入队和出队操作。
图的表示：在图的表示中，每个顶点通常包含一个指向其邻居顶点的链表。单向链表可以用于表示有向图或无向图中顶点的邻居关系。
任务调度：在任务调度系统中，可以使用单向链表来管理待执行的任务列表，通过将任务连接成一个链表，可以按照特定的顺序进行调度和执行。
多级反馈队列调度算法：多级反馈队列调度算法中，任务被分成多个优先级队列，并按照一定规则进行调度。每个队列可以使用单向链表来管理任务，实现按优先级进行任务调度。
符号表和字典实现：在符号表和字典的实现中，可以使用单向链表来存储键值对。每个节点包含一个键和一个值，并通过指针连接成一个链表，实现高效的查找、插入和删除操作。

环形链表

首尾相接的链表结构，

约瑟夫问题（Josephus Problem）：在约瑟夫问题中，有n个人围成一个环形，每次从指定位置开始计数，并按照固定规则将当前位置的人移出环形，直到最后只剩下一个人。环形链表可以用来模拟和解决这个问题。
循环队列（Circular Queue）：循环队列是一种特殊的队列数据结构，当队列的尾部达到数组的末尾时，可以绕回数组的开头，形成一个循环。环形链表可以用来实现循环队列，提供高效的队列操作。
循环链表遍历：使用环形链表可以实现循环遍历，即从任意节点开始遍历整个链表，而不会出现遍历到尾节点后的终止条件。
环形缓冲区（Circular Buffer）：环形缓冲区是一种常见的数据结构，用于在固定大小的缓冲区中循环存储数据。环形链表可以用来实现环形缓冲区，实现高效的数据读写操作。
快慢指针算法（Floyd’s Cycle Detection Algorithm）：快慢指针算法是一种使用两个指针在环形链表中寻找环的算法。该算法可以应用于检测环形链表中是否存在环以及找到环的起始节点等问题。

双向链表

双向链表是一种链表结构，每个节点都包含指向前一个节点和后一个节点的指针。

LRU缓存（Least Recently Used Cache）：LRU缓存是一种常见的缓存替换策略，其中最近最少使用的数据被淘汰。双向链表可以用来实现LRU缓存，每次访问数据时，将其移到链表的头部，这样尾部的节点就是最近最少使用的数据，可以方便地淘汰。
双向队列（Deque）：双向队列是一种具有队列和栈的特性的数据结构，可以在队列的头部和尾部进行插入和删除操作。双向链表可以用来实现双向队列，提供高效的插入和删除操作。
图的表示：在图的表示中，每个顶点通常包含一个指向其邻居顶点的链表。双向链表可以用于表示有向图或无向图中顶点的邻居关系，每个顶点可以同时保存指向前一个邻居和后一个邻居的指针。
浏览器历史记录：在浏览器中，双向链表可以用来实现浏览器的历史记录功能。每次访问一个新的页面，将其添加到链表的尾部，可以方便地实现前进和后退功能。
文本编辑器的撤销和重做操作：在文本编辑器中，双向链表可以用来实现撤销和重做操作。每次编辑操作都可以将编辑内容添加到链表的尾部，可以通过向前或向后遍历链表来实现撤销和重做操作。
音乐播放器的播放列表：在音乐播放器中，双向链表可以用来实现播放列表，每个节点表示一个音乐文件，可以方便地在当前歌曲的前后插入或删除歌曲。

前言