20220903 随机数

rand函数

1	int num = rand() % 100+1; //1~99

一般性：rand() % (b-a+1)+ a ; 就表示 a~b 之间的一个随机整数。

1位置数直接写a,100位置书要将ab差值+1

我们知道rand()函数可以用来产生随机数，但是这不是真真意义上的随机数，是一个伪随机数，是根据一个数（我们可以称它为种子）为基准以某个递推公式推算出来的一系列数，当这系列数很大的时候，就符合正态公布，从而相当于产生了随机数，但这不是真正的随机数，当计算机正常开机后，这个种子的值是定了的，除非你破坏了系统。
实现：因为rand() 的内部实现是用线性同余法做的，它不是真的随机数，只不过是因为其周期特别长，所以有一定的范围里可看成是随机的，
rand() 会返回一随机数值，范围在 0 至 RAND_MAX 间。为得到不同的随机数序列，则需改变这个种子的值。
方法：在开始产生随机数前，调用一次srand(time(NULL))

（注意：srand()一定要放在循环外面或者是循环调用的外面，否则的话得到的是相同的随机数）。

#include <iostream> 
using namespace std; 
#include <stdlib.h> 
#include <time.h> 
int main() 
{ 
    int i; 
    srand((unsigned)time(NULL)); //初始化随机数种子 
    for (i=0; i<10; i++) //产生10个随机数 
    { 
        cout<<rand()<<"/t"; 
    } 
    cout<<endl; 
    return 0; 
}

rand函数有一些问题：很多程序需要不同范围的随机数，一些应用需要非均匀分布的数。而程序员为了解决这些问题而试图转换rand生成的随机数的范围、类型或分布时，常常会引入非随机性。

srand函数

srand()用来设置rand()产生随机数时的随机数种子。
参数seed必须是个整数，通常可以利用time(0)的返回值或NULL来当做seed。
如果每次seed都设相同值，rand()所产生的随机数值每次就会一样。

随机数库

C++程序不应该使用库函数rand，而应使用default_random_engine类和恰当的分布类对象。
定义在头文件random中的随机数库通过一组协作的类来解决rand问题：随机数引擎****类和随机数分布****类。

一个引擎类可以生成unsigned随机数序列，

一个分布类使用一个引擎类生成指定类型的、在给定范内的、服从特定概率分布的随机数。

随机数引擎

随机数引擎是函数对象类，定义了一个不接受参数的调用运算符，并返回一个随机的unsigned整数。

std::default_random_engine e;
for (size_t i = 0; i < 10; ++i)
	std::cout << e() << " ";
std::cout << std::endl;

随机数引擎的操作有：

不重复的随机数序列

注意两个方面，一个是引擎的随机数序列的延后选取，一个是改变随机数发生器的种子

引擎的随机数序列的延后选取

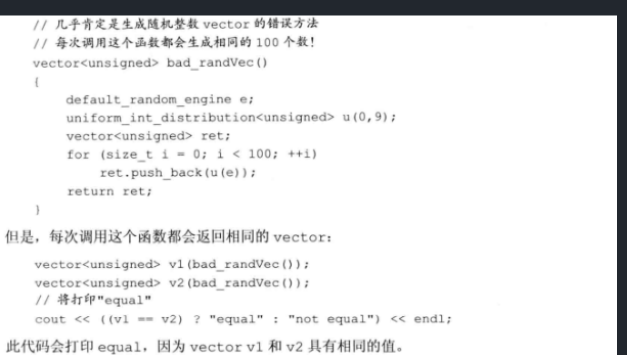
正确：

改变随机数发生器的种子

一般来说，使用time（0）获取随机种子

time(0)函数返回自格林尼治标准时间1970年1月1日00:00:00至当前时刻所流逝的秒数。

相关头文件：#include

分布类型

对于大多数场合，随机数引擎的输出是不能直接使用的，问题在于生成的随机数的值范围通常与我们需要的不符。为了得到一个指定范围内的数，我们使用一个分布类型的对象：

uniform_int_distribution：产生均匀分布的整数

std::uniform_int_distribution<unsigned> u(0, 9);
std::default_random_engine e;
for (size_t i = 0; i < 10; ++i)
	std::cout << u(e) << " ";
std::cout << std::endl;

此处我们将u定义为uniform_int_distribution。此类型生成均匀分布的unsigned值。当我们定义一个这种类型的对象，可以提供想要的最小值和最大值。

**类似引擎类型，分布类型也是函数对象类。**分布类型定义了一个调用运算答，它接受一个随机数引擎作为参数。分布对象使用它的引擎参数生成随机数，并将其映射到指定的分布。

易错：

uniform_real_distribution：产生均匀分布的实数

#include <iostream>
#include <ctime>
#include <random>
 
int main() {
 
    std::default_random_engine e;
    std::uniform_real_distribution<double> u(1.5,19.5); // 左闭右闭区间
    e.seed(time(0));
 
    for (int i=0; i<10; i++) {
        std::cout << u(e) << std::endl;
    }
 
    return 0;
}

normal_distribution：产生正态分布的实数

#include <iostream>
#include <ctime>
#include <random>
 
int main() {
 
    std::default_random_engine e;
    std::normal_distribution<double> u(0,1); // 均值为0，标准差为1
    e.seed(time(0));
 
    for (int i=0; i<10; i++) {
        std::cout << u(e) << std::endl;
    }
 
    return 0;
}

bernoulli_distribution：生成二项分布的布尔值

#include <iostream>
#include <ctime>
#include <random>
 
int main() {
 
    std::default_random_engine e;
    std::bernoulli_distribution u(0.8); // 生成1的概率为0.8
    e.seed(time(0));
 
    for (int i=0; i<10; i++) {
        std::cout << u(e) << std::endl;
    }
 
    return 0;
}

20221110 C++ 等概率数值问题

问题记录

想写一个小函数来产生等概率的0 1，但是测试发现它们这个概率并不相等

bool lrseed() {
    srand(time(0));
    if (((rand() % 1000) + 1) >= 500)return false;//左
    else return true;//右
}

问题原因

问题解决

srand(time(NULL));
num=rand()%10;
if(num==1) return 0;
else return 1;

并没有解决

1
2
3

std::default_random_engine e;
   std::bernoulli_distribution u;
   return u(e);

想用C++11中的random库来解决

并没有解决，怀疑还是引擎精度问题

//左右种子
bool lrseed() {
    clock_t start, end;
    start = clock();
    Sleep(1);
    end = clock();

    srand(end-start);
    return rand() % 2 ;

}

虽然不知道是不是产生会是等概率的，但是精度确实提高了不少，因为这个随机数的种子总能发生改变了

√

问题拓展

一

笔试代码题–C+±-输出概率相等的1和0

题目：有个输出0和1的函数（BIASED RANDOM），它以概率p输出1，以概率1-p输出0，以此RANDOM函数为基础，生成另一个RANDOM函数，该函数以1/2的概率输出1，以1/2的概率输出0

题目解答：

两次调用该RANDOM函数，如果其概率为P(x)，调用2次

P(1) = p P(0) = 1-p

P’(1) =p P’(0) = 1-p

概率如下：

11 p * p 10 p(1-p)=p-pp*

01 (1-p) p=p-pp* 00 (1-p)*(1-p)=1-2p-pp

10+01=1+p-2pp 00+11=1-2p

意思就是只选这两种模式，然后一种出现就给0，另一种给1，其他不管

函数代码如下：

//#include <random>
int random_0_1()  
{  
    int i = RANDOM();  //int i=rand();
    int j = RANDOM();  //int j=rand();
    int result;  
  
    while (true)  
    {  
        if (i == 0 && j == 1)  
        {  
            result = 0;  
            break;  
        }  
        else if (i == 1 && j == 0)  
        {  
            result = 1;  
            break;  
        }  
        else  
            continue;  
    }  
  
    return result;  
}

二从0到n-1中随机等概率输出m个不同的数

#include<iostream>  
#include <time.h>
using namespace std;
//假设输入的n远大于m
void deng(int n,int m)
{
	srand((unsigned)time(NULL));
	for(int i = 0 ; i < n ; i ++)
	{
		if (rand() % (n - i) < m)
		{
			cout << i << endl;
			m--;
		}
	}
}
int main()
{
	int n = 6, m = 3;
		deng(n,m);
	return 0;
}

理解：

1.输出m个不同的数：

由for循环n次，且满足条件时才输出数字 i，可知，输出不同数的要求已满足，因为每次输出的都是 i 值，而 i 值每次都是不一样的，m–保证了程序在输出了m个值后就不再输出i。

2.等概率：

在i=0时，rand()%(n-i)的取值范围为0到n-1，共n个数，此时要输出0只需要rand()%(n-i)小于m，故i=0被输出的概率为m/n;

在i=1时，rand()%(n-i)的取值范围为0到n-2，共n-1个数，若i=0没有被输出，则m–未被执行，此时i=1被输出的概率为m/(n-1)，若i=0已经被输出了，则m变为m-1，此时i=1被输出的概率为(m-1)/(n-1)；

由概率论的知识，可知此时i=1被输出的概率为

P=(1-m/n)(m/(n-1))+m/n((m-1)/(n-1))=m/n；

这里是两种情况

第一种是0输出且1也被输出

第二种是0未被输出然后1被输出了

以此类推，可知每个数被输出的概率都为m/n。